martes, 28 de marzo de 2017

¿Como despejar una ecuacion ?

¿ Como despejar una ecuacion?




La mayoria de las veces frente un  problema sea de Fisica, Quimica o Matematica, el despeje de ecuaciones es la falencia al resolver los problemas, por ello mostrare este ejemplo para que lo analicen y lo desarrollen por ustedes mismos.

Pasos para aprender a despejar

Lo primero que debes de saber para poder despejar una fórmula, son los siguientes puntos:Saber bien la jerarquización de las operaciones, es decir; que operación tiene más valor que otra.
  1. Agrupación
  2. Exponente y Radicación
  3. Multiplicación y División
  4. Suma y Resta
  5. Comparación
Despeje a F de la siguiente fórmula
En este caso, usaremos el ejemplo que tenemos en el artículo principal, donde tenemos la siguiente ecuación:
\displaystyle T=\frac{k-{{d}^{2}}+\frac{4\pi }{\sqrt{4F}}}{4kx+2\pi -d}
Al principio, podría parecer difícil, pero no, no lo es… 😎
Vamos a despejar todo el denominador del segundo miembro, para después multiplicarlo a T , debido a que como está dividendo, ahora en el primer miembro tendrá que pasar a multiplicar, quedando así:
\displaystyle T(4kx+2\pi -d)=k-{{d}^{2}}+\frac{4\pi }{\sqrt{4F}}
Ahora, vamos a despejar a \displaystyle \frac{4\pi }{\sqrt{4F}} que está sumando en el segundo miembro y lo pasaremos a restar al primero, quedando así:
\displaystyle T(4kx+2\pi -d)-\frac{4\pi }{\sqrt{4F}}=k-{{d}^{2}}
Ahora toda la expresión de 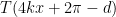\displaystyle T(4kx+2\pi -d) la pasaremos a restar al segundo miembro:
Y obtenemos lo siguiente:
\displaystyle -\frac{4\pi }{\sqrt{4F}}=k-{{d}^{2}}-T(4kx+2\pi -d)
Ahora pasamos a \displaystyle \sqrt{4F} a multiplicar al segundo miembro.
\displaystyle -4\pi =\left[ k-{{d}^{2}}-T(4kx+2\pi -d) \right]\sqrt{4F}
Después de este paso, lo más recomendable es mandar a dividir toda la expresión que acababa de pasar a multiplicar a raiz de (4F), quedando esto así:
\displaystyle \frac{-4\pi }{k-{{d}^{2}}-T(4kx+2\pi -d)}=\sqrt{4F}
Invertimos la ecuación, esto no modifica nada.
\displaystyle \sqrt{4F}=\frac{-4\pi }{k-{{d}^{2}}-T(4kx+2\pi -d)}
Pero…. \displaystyle \sqrt{4F}=2\sqrt{F} (Esto es por Álgebra básica) .
\displaystyle 2\sqrt{F}=\frac{-4\pi }{k-{{d}^{2}}-T(4kx+2\pi -d)}
Pasamos a dividir a 2, al segundo miembro.
\displaystyle \sqrt{F}=\frac{-4\pi }{2\left[ k-{{d}^{2}}-T(4kx+2\pi -d) \right]}
Podemos dividir a 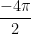\displaystyle \frac{-4\pi }{2}
\displaystyle \sqrt{F}=\frac{-2\pi }{k-{{d}^{2}}-T(4kx+2\pi -d)}
Finalmente tenemos un odioso signo negativo en nuestro numerador del segundo miembro, que vamos a eliminar multiplicando por \displaystyle \left( \frac{-1}{-1} \right)=1
Que finalmente no altero nada, porque estoy multiplicando por la unidad, es decir por 1
\displaystyle \sqrt{F}=\frac{-2\pi }{k-{{d}^{2}}-T(4kx+2\pi -d)}\left( \frac{-1}{-1} \right)
\displaystyle \sqrt{F}=\frac{2\pi }{-k+{{d}^{2}}+T(4kx+2\pi -d)}
Ahora, queda la parte más fácil, vamos a elevar ambos miembros al cuadrado, para eliminar la raíz, y dar con el resultado.
\displaystyle {{\left( \sqrt{F} \right)}^{2}}={{\left( \frac{2\pi }{-k+{{d}^{2}}+T(4kx+2\pi -d)} \right)}^{2}}
Que finalmente es:
\displaystyle F={{\left( \frac{2\pi }{-k+{{d}^{2}}+T(4kx+2\pi -d)} \right)}^{2}}
Y listo… Problema resuelto 🙂









Publicadas por a la/s

3 comentarios:

Suscribirse a: Comentarios de la entrada (Atom)